베이즈 정리: 실생활 실용적 문제해결기법

베이즈 정리

베이즈 정리(Bayes Theorem) 개요

빅데이터, AI 등의 적극적 활용과 함께 베이지안 정리(Baye’s Theorem)가 새롭게 주목받고 있습니다. 지금까지의 통계분석은 대부분 빈도주의 관점에서 반복적으로 선택된 표본이 어떤 사건의 원소가 될 경향, 즉 사건의 확률을 산출하는데 초점을 맞추어 왔습니다. 그러나 이는 어떤 가설의 신뢰도를 제시하지 못할 뿐만 아니라 새로운 정보를 반영하여 확률을 조정하는 것에도 매우 미흡하여 실제적 해결책을 찾는데 커다란 제약을 가지고 있습니다. 베이지안 정리는 이런 문제점을 극복하고 실제적인 문제해결책을 찾는데 초점을 맞춥니다.

베이지안 정리는 ‘조건부 확률’이라고도 하는데 다음과 같은 특장점을 가지고 있습니다.

확률을 상황에 따라 변할 수 있는 것이라고 생각한다. 이는 기존의 개념과 다른 것으로 추가되는 새로운 증거에 따라 확률을 새로 계산 및 개선한다.
‘이전의 경험과 현재의 증거를 토대로 어떤 사건의 확률을 추론한다’. 즉, 사전 정보를 바탕으로 어떤 사건이 일어날 확률을 토대로 의사결정을 할 때 활용된다.
다시 말해, 우리의 관심이 되는 확률을 알기 어려울 때 알고 있는 것을 바탕으로 거꾸로 계산하여 답을 찾는다.

베이지안 네트워크나 추론을 손쉽게 활용하여 보다 나은 의사결정/정책결정을 하고 성과를 높일 수 있도록 지원하는 소프트웨어, Bayesian Doctor를 한글화하여 출시하게 되었습니다. 누구나 쉽게 Bayesian Network와 Bayesian Inference를 활용할 수 있기를 기대합니다.

베이지안 이론을 활용한 확률 추론과 진단

Thomas Bayes는 확률이 상황에 따라 변할 수 있는 것이라고 생각했습니다. 이는 기존의 개념과 다른 것으로 추가되는 새로운 증거에 따라 확률을 새로 계산 및 개선합니다.

‘이전의 경험과 현재의 증거를 토대로 어떤 사건의 확률을 추론하는 알고리즘이다’.

즉, 사전 정보를 바탕으로 어떤 사건이 일어날 확률을 토대로 의사결정을 할 때 활용됩니다.

미리 알고 있는 사전확률(prior probability), 즉 A가 발생할 확률 P(A)가 있을 때, A 조건에서 B가 발생할 확률 P(B|A), 즉 우도(likelihood probability)를 활용하여 사후확률 P(A|B)를 구합니다. 사건 B를 관측한 후에 그 원인이 되는 A의 확률을 새로 산출한다는 의미로 사후확률(posterior probability)라고 합니다.
*사전확률 P(A)가 밝혀지지 않은 경우 이를 확인하는데 활용할 수도 있음

다시 말해, 우리의 관심이 되는 확률을 알기 어려울 때 알고 있는 것을 바탕으로 거꾸로 계산하여 답을 찾습니다.

이를 통해 어떤 대상에 대해서 가지고 있던 초기의 믿음을 객관적이고 새로운 정보로 업데이트할 때 개선된 새로운 믿음을 확보할 수 있습니다. (황승식, ‘불멸의 이론’ 설명 중)

베이즈 정리의 핵심

A가 발생할 확률을 P(A)라 하고, A가 발생한 조건에서 B가 발생할 확률을 P(B|A)라고 표현하면, P(B|A) = P(B∩A)/P(A)가 됩니다.

그림으로 표시하면 이해가 쉽습니다. 아래 그림에서 P(B∩A)는 (우선 전체 C에서 A가 발생해야 하므로) ‘A의 발생 확률인 P(A)’에 ‘A가 발생한 상태에서 B가 발생할 확률인 P(B|A)’를 곱하면 됩니다. 즉 P(B∩A) = P(B|A)*P(A)가 됩니다. 이항하면 P(B|A) = P(B∩A)/P(A)가 됩니다.

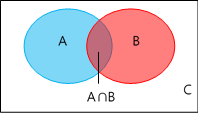
베이즈정리

즉 우리가 알고자 하는 P(B|A)를 이미 알고 있는 P(A)와 P(B), 그리고 우도 P(A|B)를 활용하여 구하였습니다.